by:
Prof. Marcelo Gattass
Computer Science Department
Tecgraf Institute
PUC-Rio, Brasil
Modeling the cinematic behavior of three-dimensional objects may include rotations as state variables.
Three-dimensional rotations is a complex subject in Computer Graphics and Numerical Simulations courses.
The simplest algebraic formulation for 3D rotations is the so-called Euler Angles.
Despite its simplicity, however, this formulation has a severe problem referenced in the literature as Gimbal Lock.
There are good explanations on the web about this problem
[Gimbal lock - Wikipedia].
This post attempts to complement these explanations with a simple web program aim to illustrate the phenomena from
a programmer's point of view.
For completeness let's review the definition of the Euler rotations and the mathematical equations that lead to the Gimbal Locak.
The model of 3D rotations with Euler angles consists of a sequence of rotations around the Cartesian axis in a given order.
Usually, the first rotation is around the x-axis, then the y-axis and last the z-axis.
The order is important because different orders yield different results.
The picture below illustrates the definition of the transformation associated with Euler angles.

This transformation has 3 degrees of freedom(DOF): the three angles around each axis. The usual argument to present the Gimbal Lock problem is based on the analysis of the matrix of the transformation. If we fix one of the DOF, the remaining transformation should still have 2 DOF. That is not what happens if we choose the y-angle to be 90 degrees. Substituting the cosine and sine of the y-angle by 0 and 1, respectively, the transformation matrix can be simplified to:
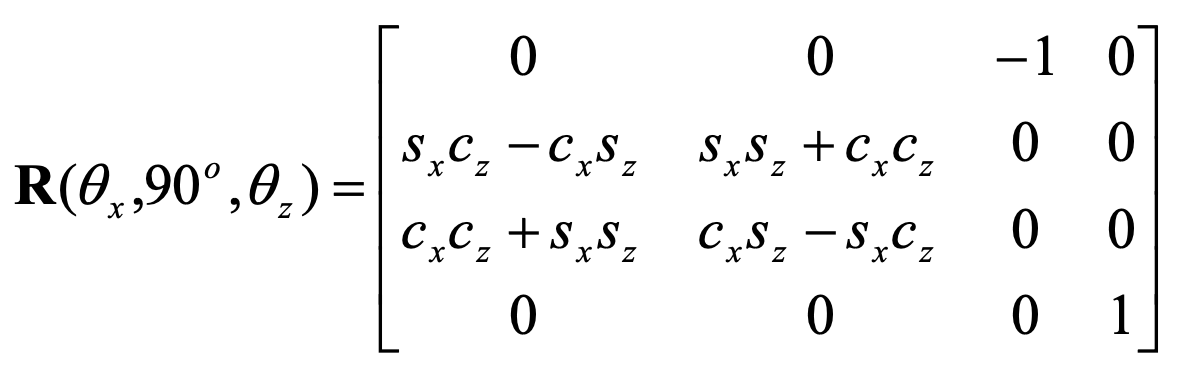
With a little trigonometry, we can see that this matrix is equivalent to:

This matrix discloses the fusion of the two remaining DOF into a single variable, one opposing the other. This explanation, however, is somewhat abstract and indirect. The problem can also be seen in geometrical terms, as we attempt to illustrate here.
Consider the teapot and the cup illustrated in the canvas below. In the javascript program, all rotations are implemented via Euler angles using the matrices illustrated above. Each time the user clicks the rotation buttons there are two possible behaviors programmed: incremental or full, depending on the toggle button shown in the interface. In the incremental procedure, the current modeling matrix is multiplied by the incremental rotation matrix, i. e., the matrix with the 5-degree angle. In the full mode, the rotation matrix computed with the full value of the angles replace the old rotation in the modeling matrix.
Try to rotate the teapot of 90-degrees in Y and then of 10-degrees in X to serve tea in both incremental and full mode.